二分查找，又叫折半查找。给定一个数据，查看该数据是否在给定的数组中，如果存在，就返回这个数据在数组中的下标位置，如果不存在，则返回-1

g需要实现二分查找的前提是：待查找的数组是有序的。

二分查找的思路：

1：需要有个有序的数组

2：需要一个待查询的数据

3：先获取的数组的中间下标的值

4：拿着中间值和待查询数据进行比较

4.1：如果中间值小于待查数据，说明，待查找的数据在中间数据的右侧后半段(因为数组有序的，折半后，右边数据大于左边数据)，所以，查询的起始位置应该是中间位置+1

4.2：如果中间值大于待查数据，说明，待查数据在中间值的左侧后半段，所以，查找位置的结束点应该是中间值下标-1

4.3：如果中间值等于比较值的话，就直接返回中间值的下标

4.4：否则就返回-1

二分查找示意图：

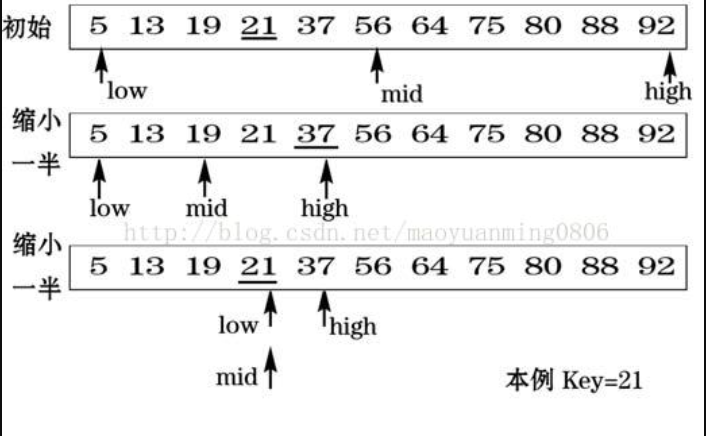
根据以上思路，可以分为两种方案：一种是递归查询的，一种是while查询的。请看代码

一：使用while方案的：

/**
 * 二分查找的真实方法
 * @param array     待查数组
 * @param compartDate   比较的数据
 * @return  比较的数据的下标
 */
public static int biSearchWhileFunction(int [] array,int compartDate){
    //起始位置
    int startIndex = 0;
    int endIndex = array.length-1;
    //中间值的下标为止
    int mIndex;
    while(startIndex <= endIndex){
        mIndex = (startIndex+endIndex)/2;
        //如果中间值== 比较值。则中间值的下表+1
        if(array[mIndex] == compartDate){
            return  mIndex ;
        }else if(array[mIndex]<compartDate){
            //如果中间值小于比较值，向右查找.也就是起始位置的下标 = 这个中间值下标+1
            startIndex = mIndex+1;
        }else{
            //中间值大于比较值，向左查询。也就是结束位置的下标 = 这个中间位置下标-1
            endIndex = mIndex-1;
        }
    }

    //未查询到数据
    return  -1;
}

第二种方案：使用递归的

/**
 * 使用递归方法的二分查找
 * @param array             有序的待查找的数组
 * @param compartDate       比较对象
 * @param minDateIndex      最小值的index位置
 * @param maxDateIndex      最大值的index位置
 * @return                  待查找对象的下标
 */
public static int recursionBinarySearchFunction(int array[] ,int compartDate,int minDateIndex,int maxDateIndex ){

    if(compartDate <array[minDateIndex] || compartDate > array[maxDateIndex]
    || minDateIndex > maxDateIndex){
        return -1;
    }
    //初始化中间位置
    int mIndex = (minDateIndex+maxDateIndex)/2;
    //中间下标值大于需要比较值的时候,需要和中间值右边比较。所以结束位置(最大值)下标 = 中间值位置下标-1
    if(array[mIndex] > compartDate){
        return recursionBinarySearchFunction(array,compartDate,minDateIndex,mIndex-1);
    }else if(array[mIndex] < compartDate){
        //中间下标值小于需要比较值的时候,需要和中间值右边比较。所以起始位置(最小值)下标 = 中间值位置下标+1
        return  recursionBinarySearchFunction(array,compartDate,mIndex+1,maxDateIndex);
    }else{
        //如果相等的话，就加1
        return  mIndex;
    }
}

测试方法：

public static void main(String[] args) {
    //二分查找。不递归方式
    int array[] = new int[]{1,3,5,7,8,10,12,15};
    int compartDate = 12;
    int dateIndex = biSearchWhileFunction(array,compartDate);
    if(-1== dateIndex){
        System.out.println("===待查询数据:"+compartDate+".在array数组中未查询到");
    }else{
        System.out.println("待查询数据："+compartDate+".在数组array中查询到了，对应的下标是:"+dateIndex);
    }

    System.out.println("==============================");
    int rDateIndex = recursionBinarySearchFunction(array,compartDate,0,array.length-1);
    if(-1== rDateIndex){
        System.out.println("===使用递归方法，待查询数据:"+compartDate+".在array数组中未查询到");
    }else{
        System.out.println("使用递归方法，待查询数据："+compartDate+".在数组array中查询到了，对应的下标是:"+rDateIndex);
    }
}

运行结果：

总结：

优点是比较次数少，查找速度快，平均性能好；

其缺点是要求待查表为有序表，且插入删除困难。

因此，折半查找方法适用于不经常变动而查找频繁的有序列表。